作者: 『同济大学数学老外卖』
引言
本测试有四不写
没学高数和线代者不写,
因为它难. 还没学就写指定这辈子都不想学高数和线代了.
高数线代没学完者不写,
因为它多. 没学完就写都不知道知识点在哪.
高数线代学完者不写,
因为它长. 都学完了还写他干嘛该干嘛干嘛去.
玩原神者不写, 不因为啥.
毕竟都玩原神了,不能要求太高.
第一题
本题是为了解决一类Taylor展开式的计算问题,进而求一些特别的极限.
第一小问
已知无穷次可微函数的带Peano余项的Taylor展开式为
可以用以下方法求函数的Taylor展开式. 注意到,
对等式两侧同时求次导数,
并对等式右侧使用Leibniz公式. 设是的Taylor展开式中的项系数, 证明:
第二小问
使用第一小问中的公式, 计算函数的Taylor展开式的前二项,
并求极限:
第二题
本题是计算算术-几何平均值.
对于, 记为的算术平均值, 为的几何平均值. 由基本不等式知,等号成立当且仅当.
下面用这两种均值构造一种新的平均值.
设.
由以下的递推公式定义数列:
第一小问
显然是单调递增数列,
而是单调递减数列. 证明:
.
从而说明和收敛于同一值. 这个值就称为的算术-几何平均值, 记为.
第二小问
Gauss给出了用一类积分来计算算术-几何平均值的方法. 设是如下定义的积分
为计算这个积分.进行换元:
证明:
并用表示.
第三小问
虽然第二小问中的没有具体的解析式.
但是这种积分经常出现在许多计算当中. 例如下图所示, 两个无限长的圆柱轴线垂直相交于原点,
半径分别为和, 求它们相交部分的体积, 结果用来表示.
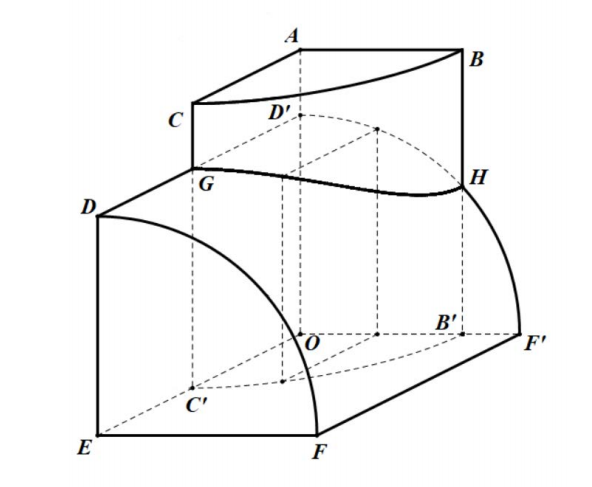
第二题第三小问图
第三题
本题是通过几何方式证明一个秩不等式,
并指出秩不等式的取等条件.
记为阶矩阵, 考虑秩不等式
设分别是维向量空间,下面也用以及代表这些矩阵对应的到的线性映射. 用核空间维数代替秩,
原不等式等价于
注意到, 任取, 有. 从而, 即. 于是,
故有
容易发现等号成立当且仅当以及.
于是可以如下选取的一组基:
先选定为的一组基,
先将其扩充为一组基,
再将其扩充为的一组基. 此时有. 接下来选定的一组基.
第一小问
首先需证明: 限制在上是一个可逆映射,
因此可以选取个维向量, 使得在这两组基下的矩阵为. 同理可以选取个维向量, 使得在这两组基下的矩阵为.
第二小问
使用条件, 证明:
第一小问中选取的是线性无关的.
从而可以添加,
扩充成为维向量空间的一组基.
于是在基和下, 的矩阵分别为
从而秩不等式成立的充要条件为: 存在阶和阶非奇异矩阵,使得
并且
第四题
本题证明一个关于迹零矩阵的重要事实,
其在李代数的研究中格外重要.
记阶实矩阵空间为, 定义上的迹函数为
因是线性的,
故使得的矩阵构成一个线性空间, 记为. 下面对进行刻画.
第一小问
设, 证明.
从而任意形如的矩阵都在中. 特别地, 设是这些矩阵张成的子空间, 即 是的一个子空间.
第二小问
下面求出的一组基. 设是第位置为, 其余位置为的阶方阵. 于是任取,
有
此处注意到, 如果是对称矩阵,
那么有
从而是的线性组合.
注意到任意矩阵都能写成一个对称阵和一个反对称阵之和, 据此证明:
是的一组基.
容易发现这也是的一组基,
从而有. 于是方阵迹为零当且仅当存在方阵,使得
第五题
本题是研究质点在平面和空间中的运动问题.
因此本题中的符号依照物理学的习惯.
假设质点在平面内运动, 其在时刻的位置向量为,
位置向量和正半轴的夹角为. 于是质点在时刻的速度可以表示为
这里在函数上方加一点表示其对的导数, 之后加两点表示对的二阶导数, 依此类推.
质点的加速度即为
质点在时间内走过的弧长为
第一小问
考虑质点的切向加速度. 即加速度在垂直于速度的方向的投影, 即为
证明:
这里为质点的运动轨迹在点处的曲率. 这个等式表明,
质点在时刻的瞬时运动即为在曲率圆上作变速圆周运动.
第二小问
使用第一小问的结论解决物理问题. 如图质点位于原点处, 有形状为的光滑轨道.
现予质点一向右的初速度,
使质点向前滑行. 为使质点始终不脱离轨道, 求应该满足的条件.
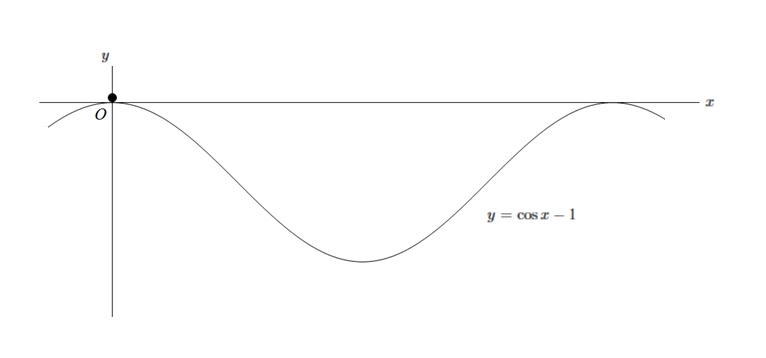
第五题第二小问图
第三小问
现在考虑质点在空间中的运动.
试证明第一小问的结论对于空间中的运动仍然成立.
现有一垂直于地面的光滑椭圆柱内侧面, 其关于的参数方程为
一质量为的质点位于点处.
现予质点一垂直于椭圆柱面的初速度,使质点在重力的作用下沿椭圆柱面做螺旋线运动.
求质点运动轨迹和椭圆柱面受到的压力.
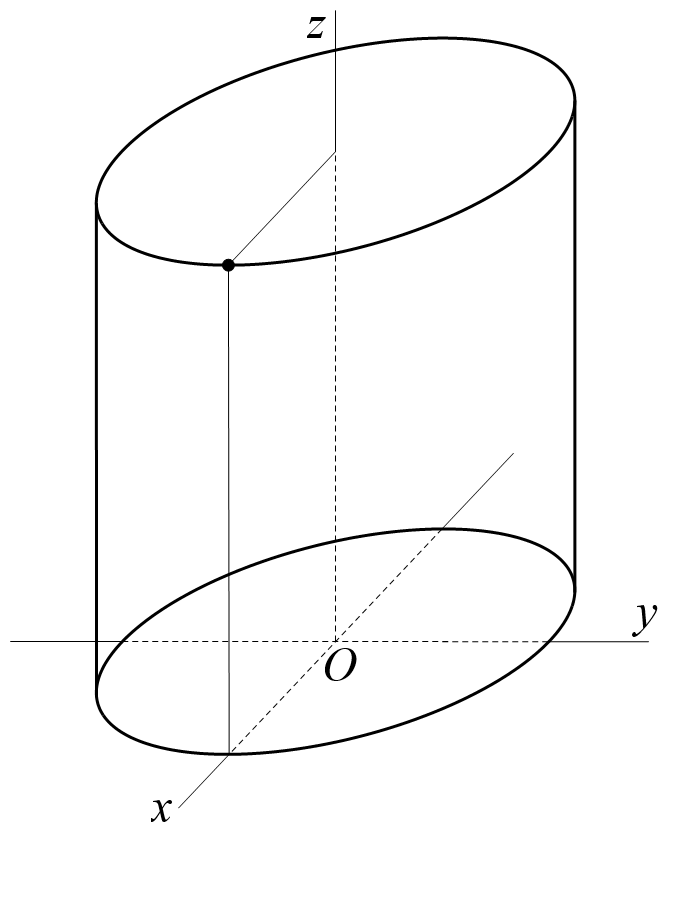
第五题第三小问图
第六题
本题是求解一类矩阵的特征值, 并尝试着给出它的几何意义.
本题表明寻找矩阵的几何意义有时给予我们额外的注意力.
第一小问
记是维实线性空间, 定义是由如下的集合生成的线性空间.
将集合中的向量记为, 将由生成的子空间记为. 证明.
第二小问
由第一问的结论, 中的向量可以写成若干个的线性组合的形式. 设是上的线性变换, 定义上的线性变换为
这里.
给定一组基, 写出这组基下的矩阵.
第三小问
为求的特征值,先计算两个例子.
当时, 设,
此时在第二小问中取好的基下,的矩阵为
证明: 的特征值为.
这里是的特征值.
又设是对角矩阵,此时的矩阵为
这里依惯例代表第位置为,其余位置全为的阶方阵. 利用Laplace展开式分别对行, 行, 直至行展开, 计算其特征值.
第四小问
根据第三小问的结论猜测的特征值. 如果没有这个几何模型,
直接通过矩阵计算求的特征值,
是不容易想到的. 但是这个几何模型给了我们很好的思路. 首先容易注意到:
若是的属于特征值的特征向量, 那么有
从而一定有属于的特征值. 类似地, 若分别为的属于特征值的特征向量, 那么不是的特征向量, 而是的特征向量:
于是我们对半单矩阵(即有个线性无关的特征向量), 进行证明.
首先证明: 也为半单矩阵,
从而的特征值为
以及
这里是的特征值, .
再计算的特征值.
对非半单的矩阵, 注意到半单矩阵在阶矩阵空间中是稠密的,
而行列式函数是连续函数, 从而上述结论适用于全体矩阵.
第七题
本题是利用Abel求和方法计算两个极限.
本题表明无穷积分的计算的某些方法有时候对无穷级数的计算也有效果.
Abel求和法也称分部求和法,意味着它和积分运算中的分部积分法有相似之处.
设是两数列, 是的前项和, . 那么有
第一小问
考虑. 其在上的无穷积分是不存在的.
但是可以使用特殊的方法使其收敛. 考虑积分
这个积分在时是收敛的.
因此可以考虑极限. 考虑另一积分
这个积分在时同样是收敛的,
也可以考虑极限.
下面试求这两种积分的值.
证明: 无穷积分
收敛, 由此说明.
第二小问
使用和第一小问同样的方法, 证明在时, 无穷积分
收敛, 并且.
第三小问
对应地, 现在考虑数列. 显然也不收敛.
同样可以使用特殊方法使其收敛. 考虑数列
和
它们在时同样是收敛的.
因此想到猜测
但直接计算这两个数列是困难的, 特别是, 它无法使用初等解析式表达出来.
但是前两小问的计算给了我们启发:
尽管前两小问的计算中并没有求出被积函数的原函数,
但是还是使用了分部积分法完成了计算. 因此此时应该对应地使用Abel求和法.
这需要一点准备工作.
首先使用欧拉公式
这里是虚数单位,
将写成两个等比数列之和,
从而进行求和. 证明正弦等差数列求和公式:
第四小问
以为例,
使用Abel求和法进行计算:
代入第三小问中的公式, 得
使用和差化积公式, 上式等于
从而得
模仿上述计算,求证
第八题
本题对一个常见的矩阵方程的解进行分析.
设是阶方阵, 常常考虑与可交换的方阵, 即矩阵方程
的解. 注意到这是一个线性方程, 因此所有与可交换的方阵构成的线性空间就是这个方程的解空间.
现研究这个解空间.
第一小问
下面定义两种运算. 矩阵的拉直映射是阶矩阵空间到维列向量空间的线性映射, 定义如下
对于阶矩阵和阶矩阵,定义它们的Kronecker积为
是一个阶矩阵. 证明: 对阶矩阵和阶矩阵, 有
这里分别是阶单位阵.
第二小问
对方程两边同时进行拉直,
就有
于是矩阵方程的解空间维数就等于. 下面尝试用的性质来计算. 用分块矩阵的性质说明:
这里分别是阶矩阵.
第三小问
现在可以对进行相似上三角化. 设是可逆矩阵, 分别将上三角化:
记这两个上三角矩阵分别为, 那么有
证明: 也是上三角矩阵,且对角元就是.
记是两两相同的特征值的组数, 那么有估计
也即矩阵方程的解空间维数大于等于.
第四小问
证明: 第三小问的估计对半单矩阵是精准的, 即当为半单矩阵的时上述不等式取等号.
但是对非半单的矩阵估的估计不精准. 令
并选取相应的可逆矩阵,使得. 使用第三小问的不等式估计,
得
计算的真实值, 从而说明上述的估计是不准确的.
第五小问
用类似的方法可以得到一个经典结论: Sylvester矩阵方程
存在唯一解的充要条件是没有相同特征值. 试证明之.
第九题
本题是计算一个极限,
并运用类似的计算方法证明Riemann-Lebesgue引理的一个简单情况.
第一小问
记函数
这个瑕积分是绝对收敛的, 并且. 下面叙述一种方法证明在处可微. 因是奇函数,因此只需证明在处右导数存在. 这等价于证明极限
存在. 将上式中的积分记作.
现将无穷积分拆分为在区间上区间积分的无穷和, 即
因为是绝对可积的,
因此上述拆分是合理的. 用诱导公式, 得
证明: 对, 有
由此说明
从而得证可微性, 并且.
第二小问
上面处理的积分可以做如下变形:
于是我们可以考虑更一般的情形. 设在上绝对可积, 则有
不妨先考虑有限区间上的情形, 设在上是可积的, 那么
这里. 于是
这里是在上的上界(因为是可积的, 因而有界).
上式中的第一项有
这里
是的振幅.
使用的可积性证明: 有与无关的上界, 从而上式极限为0.
这就是(Riemann可积情形的)Riemann-Lebesgue引理.
第三小问
下面证明无穷积分的Riemann-Lebesgue引理. 由绝对可积,知对任意, 存在, 使得
用有限区间的Riemann-Lesbegue引理完成证明.
PDF下载
由于网站上对某些符号不支持,甚至与某些Latex代码有冲突,尤其是物理背景的这一题,会有字体不统一的情况出现.而PDF文件可以点击此处下载.


