作者: 21级数拔 戴云舒

引言

有这么一个问题,在我们的QQ线上答疑群上出现了很多次.而我们勤劳的杨磊讲师,总是会掏出他的那个『包浆反例』来回答:

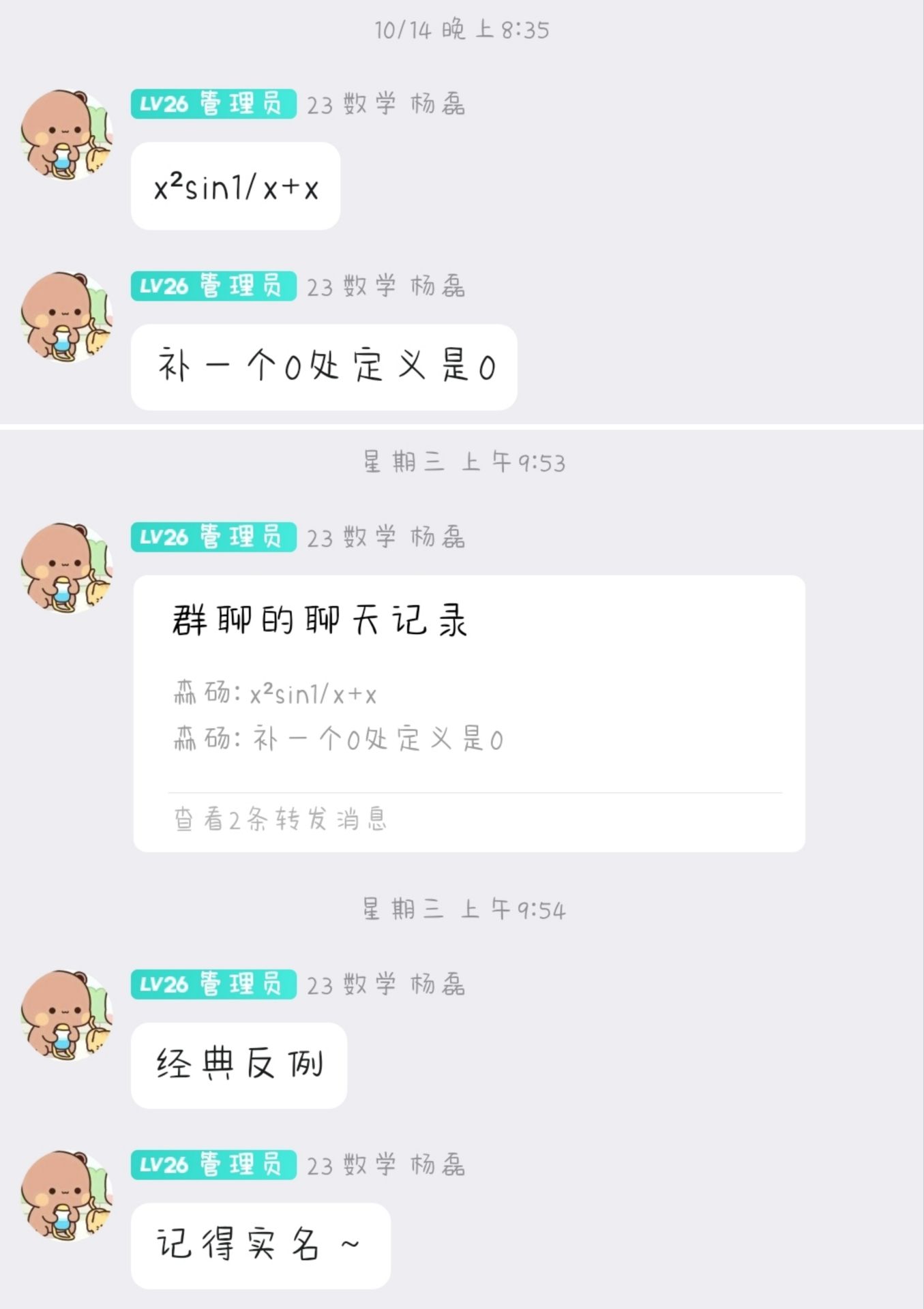
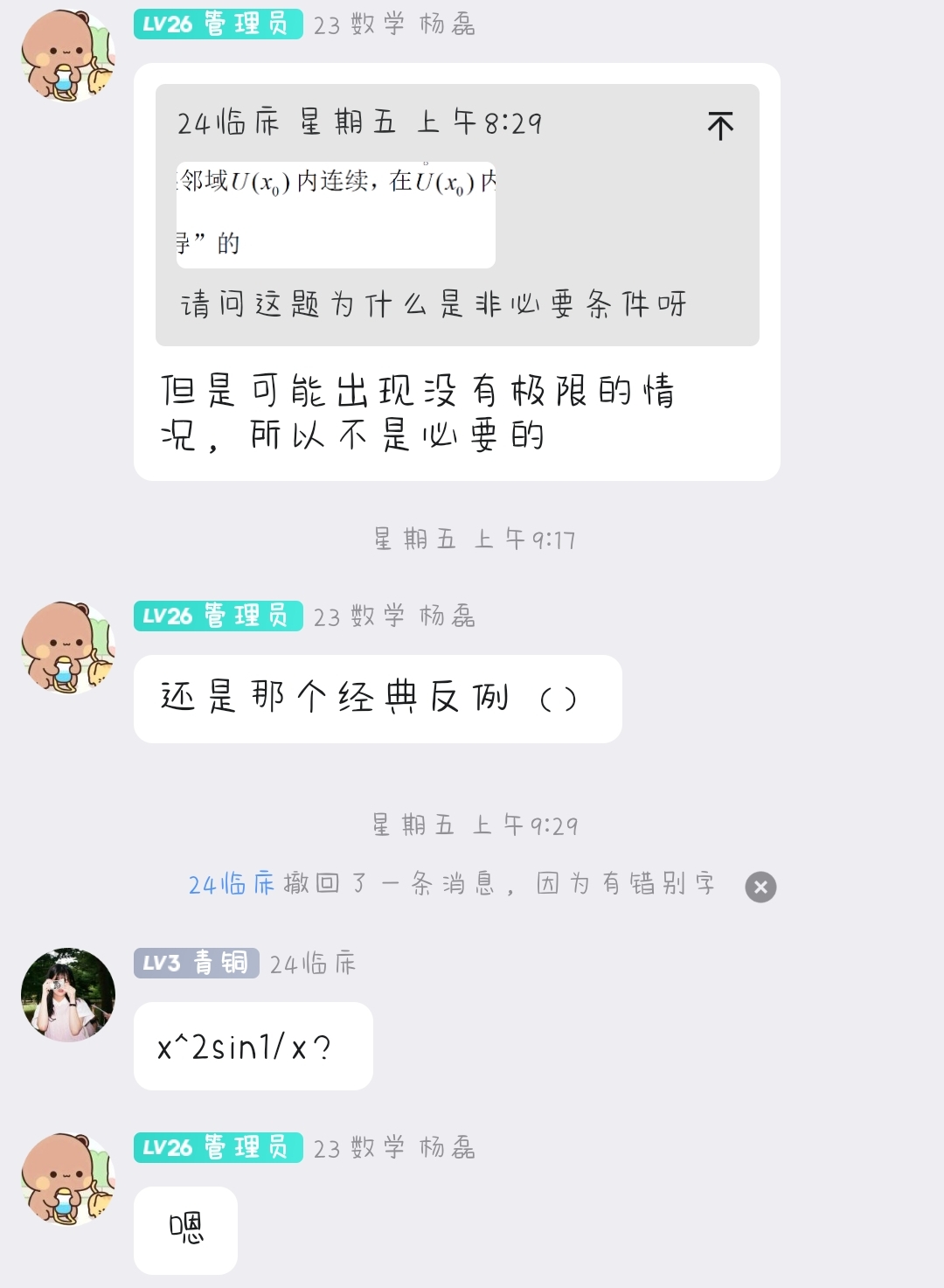
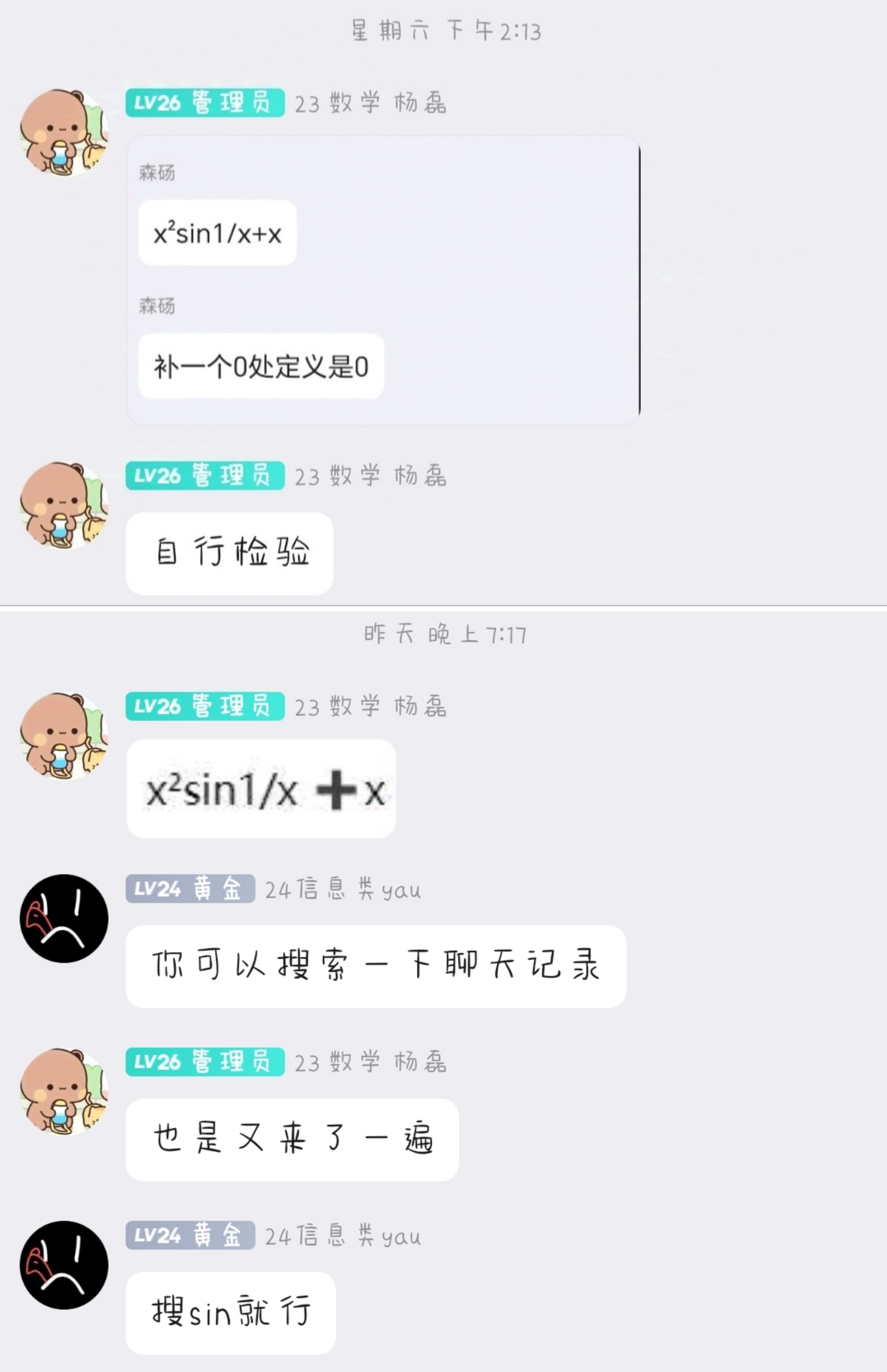
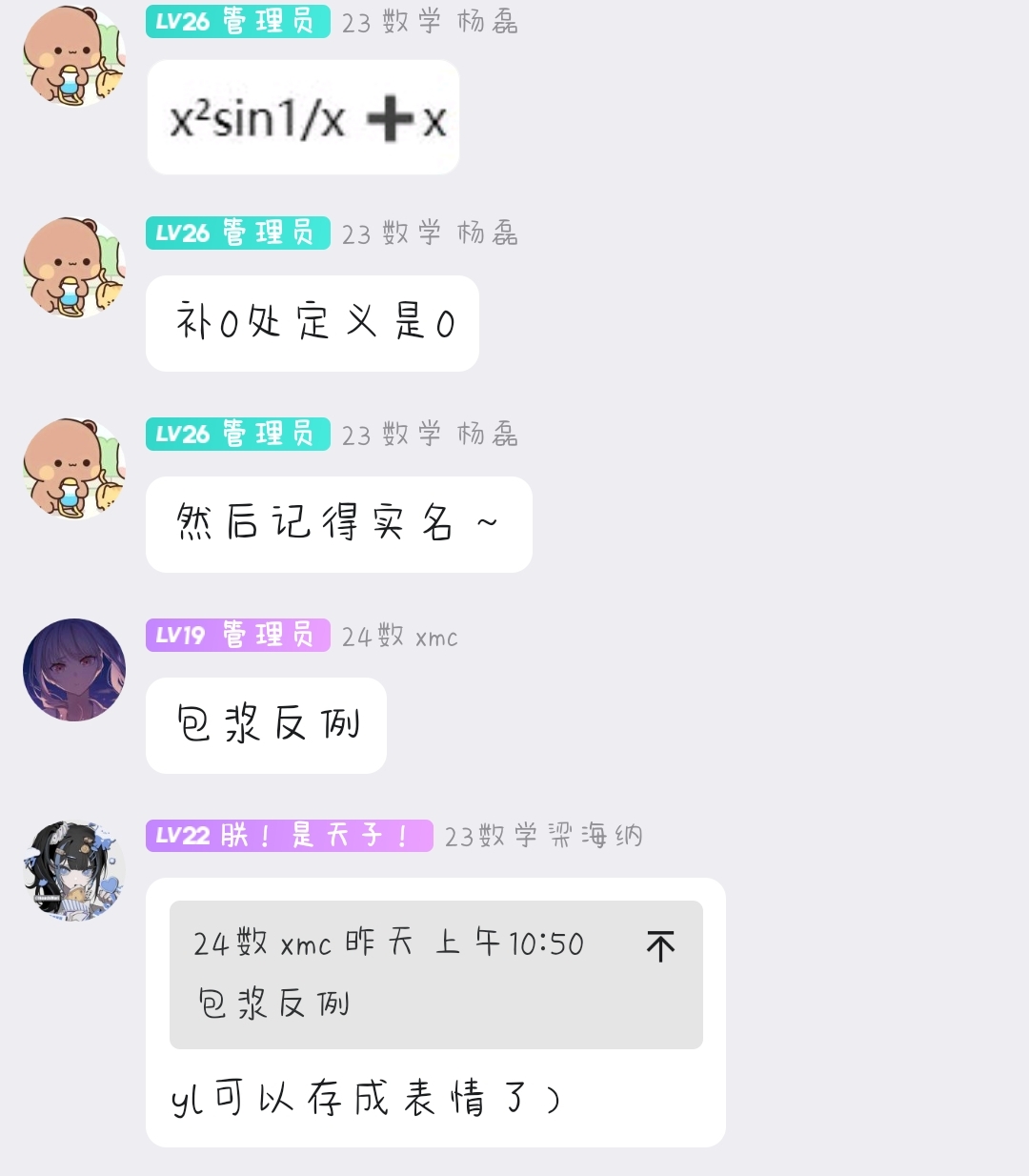
该反例甚至都已经会抢答了!因此,杨磊讲师完全可以称为『』专属代言人!恭喜!🥰🥰🥰

而这个问题便是:

设函数在的某邻域内连续,在内可导.
那么为什么『极限存在』是『在处可导』的充分不必要条件?
反例怎么找?

代言人本人认为大家可以直接看汪林的《数学分析中的问题和反例》,因此一开始并未考虑加入有趣的小题系列,但是出现频率实在太高了(看上面的图大家也能够知道),而且也可以在本文中系统分析一下两者的区别.之后有趣的小题也可能以这种内容与方式更新!

如果知道以下知识可能更容易理解: 极限和导数

适合人群: 主要针对学高数的同学

后续我们也会不定时推送有趣的小题系列,并且更偏向于数学学习过程中涉及到的概念和知识点的巩固与深入,有可能是对高数书上某个有趣概念的解释,也有可能是大家做过的某个有趣题目的深入与推广,形式则是像本文一样为问题或知识点+讲解+思考题.因此本系列并不是经典错题的收集与整理(如果数学外卖还忙得过来的话也不是不行,所以快快加入数学外卖!),感兴趣的同学可以多多关注!

问题解答

我们先来证明『极限存在』是『在处可导』的充分条件,而工具便是拉格朗日中值定理:

在处的左导数为:

由拉格朗日中值定理便知:

则由条件存在可知,也存在.

对在处的右导数也是同样的方法讨论.最后验证左右极限相等,于是可证得在处可导.

从而『极限存在』是『在处可导』的充分条件.

然后我们以 为例来说明这并不是一个必要条件:

的图像

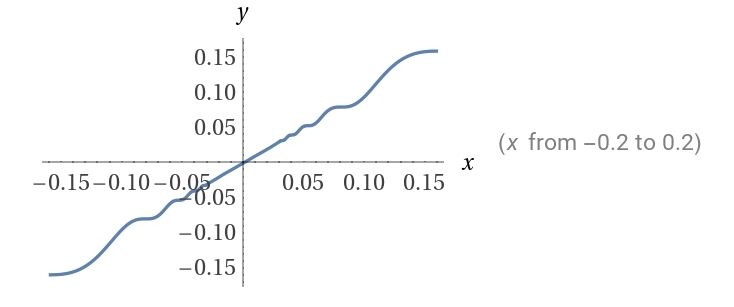
我们先求出的导函数,

在处:

而在处:

[注意,在处的导数必须得通过定义来计算,想想『在一点处求导数』的定义]

从而可以得到的导数:

因此在处是可导的,导数为.但是由于的存在,并不存在.

从而『极限存在』并不是『在处可导』的必要条件.

两者的差别

现在我们再来仔细辨析两者的区别.我们已经知道的是,导数的几何含义差不多就是在这个点处的切线的斜率,实际上,『在处可导』看重的还有处的值;而『极限存在』则不看重处的值,而更重视的是处去心邻域的『光滑』情况.

现在我们用这样一个带有可去间断点的函数 去解释一下两者的区别:

我们先来看看在处的情况,也就是在附近的切线(红色部分):

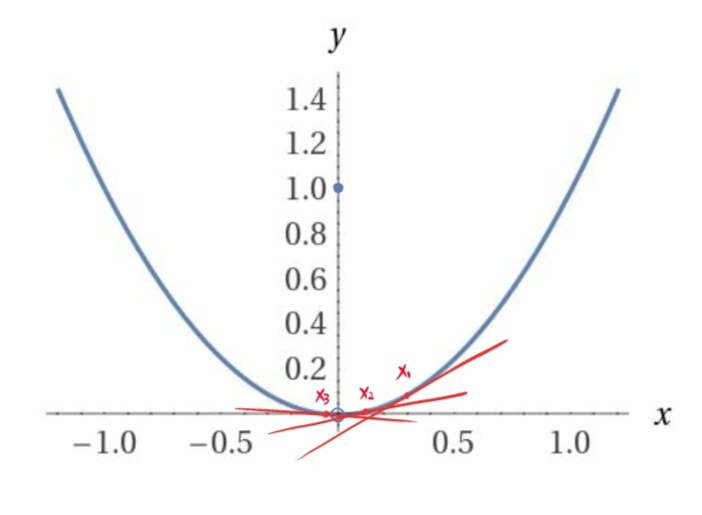
也就是说,当越来越趋近于&0&时,其切线的斜率也是趋近于的,即:,这和的事实完全没有关系.因此说:『极限存在』不看重处的值,更重视的是处去心邻域的『光滑』情况.

然后我们再来对比一下另一种情况,也就是,而,而后面代表的是以下红线的斜率:

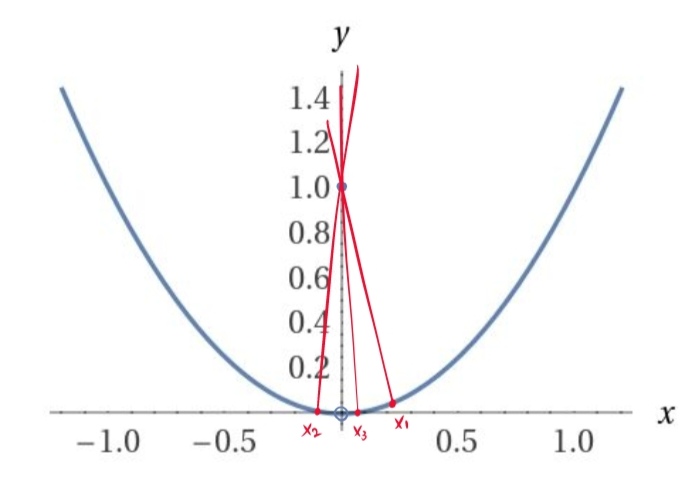
注意看,当趋近于时,红线的斜率总是在往走,即:在处是不可导的.因此说:『在处可导』看重的还有处的值.

如果对上述说法还有疑惑的话!罚你去把导数的定义抄十遍!(不是)

『包浆反例』的另一适用情况

如果你认为 只能作为上述讨论问题的反例,那你就大错特错了.因为至少在群里还有一个问题,它的反例也可以用这个的修改版来说明.而这个问题是:

设函数连续,且,则存在,使得:( )

A. 在内单调增加 B. 在内单调减少

C. 有 D. 有

而对于选项A而言,杨磊讲师所代表的函数也是它的最佳反例了.(不能直接使用这个反例,感谢群友的指正,这下作者要去抄导数的定义了😭)

对于选项A而言,杨磊老师代言的函数稍加修改后就能说明了,我们只需把它修改为 或者 就行了.然后可以去验证在内总是有正有负的,不论取多小的正数,从而不可能在上单调了.因此这个反例的构造形式是很重要的,它将一个连续的原函数与一个震荡不连续的导函数联系起来,因此大家可以多留意留意这样的构造形式.

以下是的导函数的图像:

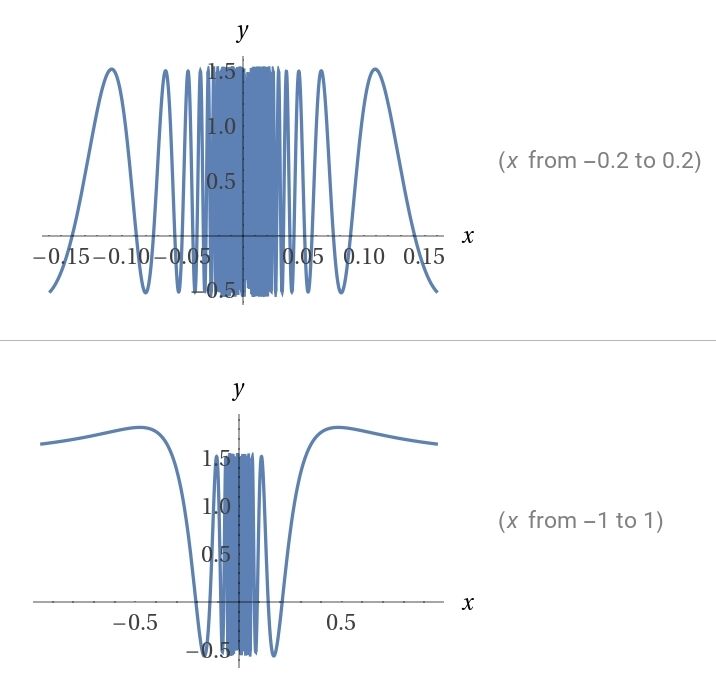
因此在一个区间内的单调性,实际上也不是由一个点处的导数值所决定的了,而是整个区间内的导数值.

如果你还发现了文章中的问题,都可以指出并在群内提醒!我们难免也会有笔误,或者是像本次一样的想当然😭,都请大家多多批评指正!

思考题!!!

完成”『极限存在』是『在处可导』的充分条件”证明中所省略的最后两步(加黑的两步).

完成最后一道选择题,并且对选出的选项能够完全证明(还是导数的定义!!!).